Função ou Equação de Segundo grau
Equação de Segundo grau é a função real do tipo y= ax2+bx+c, sendo a, b e c constantes e a ≠0.
Exemplos:
y= x2+3x+1
a=1
b=3
c=-1
y= -x2+5
a=-1
b=0
c=5
y= x + 3x2
a=3
b=1
c=0
—
Zero ou Raízes da Equação de de Segundo grau
—
As raízes ou zeros da equação de segundo grau, y= ax2+bx+c, caso existam, são os valores de x quando y=0.
Desse modo, para resolver fica: ax2+bx+c=0
—
Assim, para encontrarmos as raízes devemos usar a fórmula de bhaskara:
Visto que Δ=b2-4ac
—
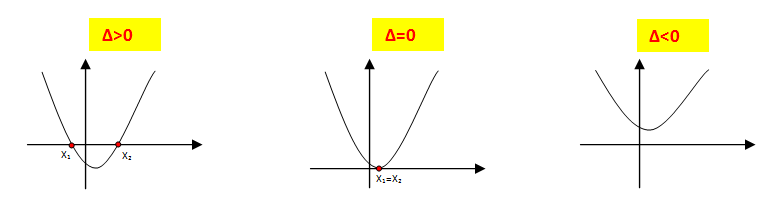
OBS.: Dessa maneira, o número de raízes da equação de segundo grau depende do valor de Δ:
1) para Δ>0 – Duas raízes reais e distintas
2) para Δ=0 – Duas raízes reais e iguais
3) para Δ<0 – não possui raiz real
—
Exemplo de gráficos:
—
—
Quando a equação de segundo grau for incompleta, ou seja, b ou c são iguais a 0, podemos resolver a equação de segundo grau de outras formas:
—
a) Quando c=0, ou seja, y=ax2+bx
Podemos resolver colocando o x em evidência.
ax2+bx=0
x(ax+b)=0
Com isso para essa equação ser igual a 0:
x=0 ou ax+b=0
ax = -b
x = -b/a
—
Exemplo: y = x2 + 2x
x2 + 2x = 0
x(x+2) = 0
Assim, x=0 ou x+2=0
x=-2
Logo as raízes são x1 = 0 e x2 = -2
—
b) Quando b=0, ou seja y=ax2+c
ax2+c=0
ax2=-c
x2=-c/a
Exemplo: y=25-x2
25-x2=0
x2=25
x =±5
Então as raízes são x1=5 e x2=-5
Gráfico da Equação de segundo grau
—
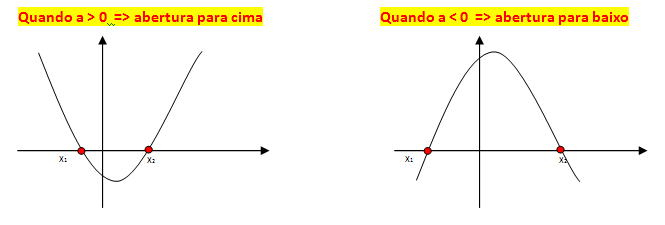
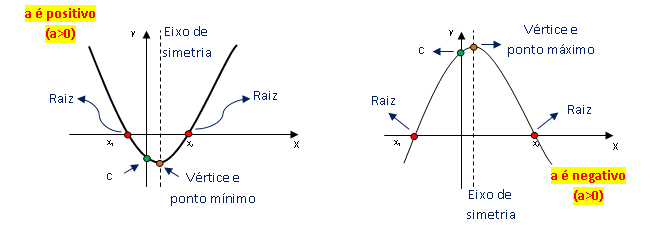
A gráfico da equação de segundo grau tem forma de parábola. A abertura ou concavidade da parábola é definida pelo valor de a:
– O ponto mais alto (máximo) ou mais baixo (mínimo) da parábola é o vértice.
—
– A reta vertical (imaginária) que passa pelo vértice é o eixo de simetria.
—
– O valor do coeficiente c, no gráfico é o ponto em que o gráfico cruza o eixo y. Pois sabendo que y = ax2+bx+c, então quando x=0, teremos y = 0.x2+0.x+c. Assim, y=c.
—
Dessa forma, só de olhar um gráfico temos várias informações:
—
Cálculo do vértice da parábola
—
Através do vértice determinamos o ponto máximo e o ponto mínimo da função e desse modo conseguimos analisar o crescimento e decrescimento da função. Assim, os pontos do vértice são (Xv, Yv), em que Xv e Yv são definidos como:—
—
Soma e Produto das Raízes
—
A soma S e o Produto P de duas raízes X1 e X2 dependem dos coeficientes a, b e c da equação de segundo grau.
Demonstração:
—
Em resumo, o que você precisa saber é:
S= -b/a e P= c/a
Exemplo: Qual a soma e o produto das raízes da equação y=x2-7x+6?
a=1, b= -7 e c= 6
S= x1 + x2 = -b/a = -(-7)/1
S= 7
P= x1 . x2 = c/a = 6/1
P=6
Espero que tenha gostado do conteúdo e principalmente tirado suas dúvidas. Mas se ainda ficou com alguma dúvida deixe um comentário.
Agora é hora de praticar! Clique AQUI e veja as questões resolvidas de Equação de Segundo Grau que separamos para você.
Quero ficar por dentro das dicas
Cadastre-se aqui e fique por dentro das nossas dicas para passar no ENEM e concursos. Ainda receba as 7 dicas MATADORAS para passar no ENEM.
Fique tranquilo. Nós não enviamos spam

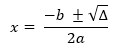
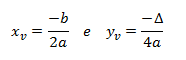
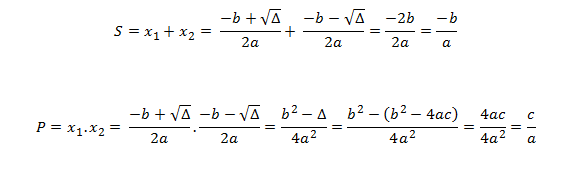
Deixe um comentário