Quer garantir algumas questões em matemática no ENEM? Então você precisa saber a diferença entre média, moda e mediana. Sempre cai uma ou mais questões sobre isso. Essa á parte de estatística que geralmente cai no ENEM.
As questões geralmente são bem simples. Você só precisa saber o que é média, moda e mediana para resolver essas questões.
Então vamos lá:
Média
Média aritmética simples: quando se fala em média, geralmente é a média aritmética e é obtida somando os valores de todos os dados e dividindo a soma pelo número de dados envolvidos.
Exemplo: As notas de um aluno durante o ano foram 6, 7, 5, 8 e 7. A média desse aluno é:
Para calcular a média vamos somar todas as notas (6+7+5+8+7) e dividir pela quantidade de notas, no caso é 5.
Média ponderada já ocorre quando os valores tem pesos (importância) diferentes e é calculada através do somatório das multiplicações entre valores e pesos divididos pelo somatório dos pesos.
Exemplo: As notas de um aluno durante o ano foram 6, 7, 5, 8 e 7. As quatro primeiras notas tem peso 1 e a última nota tem peso 2. Qual a média ponderada desse aluno?
Como dito acima, a média ponderada será o somatório das multiplicações entre os valores e pesos divididos pelo somatório dos pesos:
Moda
É o valor mais frequente de um conjunto de dados, ou seja, é o valor que mais se repete.
Exemplo: As notas de um aluno durante o ano foram 6, 7, 5, 8 e 7. Qual a moda das notas desse aluno?
A moda desse aluno é 7, pois é o valor que aparece mais vezes. (Duas vezes).
Mediana
É o valor central de um conjunto de dados.
Para calcular a mediana, você deve primeiro ordenar os valores por ordem crescente ou decrescentes. Depois de ordenado, a mediana será:
– o valor que ocupa a posição central, se a quantidade desses valores for ímpar.
– a média dos dois valores centrais, se a quantidade desses valores for par.
Exemplo: As notas de um aluno durante o ano foram 6, 7, 5, 8 e 7. Qual é a mediana da nota desse aluno?
Para achar mediana, primeiro devemos ordenar as notas: 5, 6, 7, 7, 8
Como a quantidade de notas é ímpar a mediana será o valor central, no caso 7.
Vejamos agora alguns exemplos de média, moda e mediana nas provas do ENEM:
1) ENEM 2014 – Os candidatos K, L, M, N e P estão disputando uma única vaga de emprego em uma empresa e fizeram provas de português, matemática, direito e informática. A tabela apresenta as notas obtidas pelos cinco candidatos.
|
Candidatos |
Português | Matemática | Direito | Informática |
| K | 33 | 33 | 33 | 34 |
| L | 32 | 39 | 33 | 34 |
| M | 35 | 35 | 36 | 34 |
| N | 24 | 37 | 40 | 35 |
| P | 36 | 16 | 26 | 41 |
Segundo o edital de seleção, o candidato aprovado será aquele para o qual a mediana das notas obtidas por ele nas quatro disciplinas for a maior.
O candidato aprovado será
A) K
B) L
C) M
D) N
E) P
Resolução:
A questão está querendo saber quem tem a maior mediana de suas notas. Para isso teremos que colocar as notas de cada candidato em ordem crescente.
| K | L | M | N | P |
| 33 | 32 | 34 | 24 | 16 |
| 33 | 33 | 35 | 35 | 26 |
| 33 | 34 | 35 | 37 | 36 |
| 34 | 39 | 36 | 40 | 41 |
Como a quantidade de notas de cada candidato é par (4). A mediana será a média dos elementos centrais, ou seja, a soma do 2⁰ e 3⁰ elementos divididos por 2.
| K | L | M | N | P | |
| Mediana | 33 | 33,5 | 35 | 36 | 31 |
Assim, o candidato que tem a maior mediana é N. Letra D.
2) ENEM 2014 – Ao final de uma competição de ciências em uma escola, restaram apenas três candidatos. De acordo com as regras, o vencedor será o candidato que obtiver a maior média ponderada entre as notas das provas finais nas disciplinas química e física, considerando, respectivamente, os pesos 4 e 6 para elas. As notas são sempre números inteiros. Por questões médicas, o candidato II ainda não fez a prova final de química. No dia em que sua avaliação for aplicada, as notas dos outros dois candidatos, em ambas as disciplinas, já terão sido divulgadas.
O quadro apresenta as notas obtidas pelos finalistas nas provas finais.
| Candidato | Química | Física |
| I | 20 | 23 |
| II | X | 25 |
| III | 21 | 18 |
A menor nota que o candidato II deverá obter na prova final de química para vencer a competição é
A) 18
B) 19
C) 22
D) 25
E) 26
Resolução:
Como vimos a média ponderada, é a média em que os valores tem pesos diferentes entre si. E é calculada através do somatório das multiplicações entre valores e pesos divididos pelos somatórios dos pesos.
Nessa questão temos que as notas de química tem peso 4 e as notas de física tem peso 6. O somatório dos pesos é 10, ou seja, 4 + 6.
Primeiro vamos calcular a média ponderada do candidato I e do candidato III:
– Média ponderada candidato I:
– Média ponderada candidato III:
Para que o candidato II vença a competição ele deve ter uma média ponderada maior que 21,8.
4X + 150 > 218
4X > 218 – 150
4X > 68
X > 68/4
X > 17
Assim, a menor nota que o candidato II precisa tirar é 18.
LETRA A
3) ENEM 2014 – Uma loja que vende sapatos recebeu diversas reclamações de seus clientes relacionadas à venda de sapatos de cor branca ou preta. Os donos da loja anotaram as numerações dos sapatos com defeito e fizeram um estudo estatístico com o intuito de reclamar com o fabricante.
A tabela contém a média, a mediana e a moda desses dados anotados pelos donos.
| Estatística sobre as numerações dos sapatos com defeito | |||
| Média | Mediana | Moda | |
| Numerações dos sapatos com defeito | 36 | 37 | 38 |
Para quantificar os sapatos pela cor, os donos representaram a cor branca pelo número 0 e a cor preta pelo número 1. Sabe-se que a média da distribuição desses zeros e uns é igual a 0,45.
Os donos da loja decidiram que a numeração dos sapatos com maior número de reclamações e a cor com maior número de reclamações não serão mais vendidas.
A loja encaminhou um ofício ao fornecedor dos sapatos, explicando que não serão mais encomendados os sapatos de cor
A) branca e os de número 38.
B) branca e os de número 37.
C) branca e os de número 36.
D) preta e os de número 38.
E) preta e os de número 37.
Resolução:
Informações do enunciado:
– Pela tabela temos que o número que mais apresenta reclamações é o 38, pois este é a MODA.
( Assim já poderíamos eliminar as letras B, C e E)
– Foi dito no enunciado também que foi feita uma média da distribuição da cor dos sapatos, em que branco = 0 e preto = 1. Ou seja, foi realizada a soma de todos os 0 e 1 (sapatos brancos e pretos) e dividido pelo numero total de sapatos.
Como a média deu 0,45, como informado, e 0,45 é mais próximo de 0 do que de 1. Podemos afirmar que existiam mais sapatos brancos do que preto com defeito, ou seja, existiam mais 0 do que 1.
Assim, o sapato que apresenta mais defeito é o branco 38, letra A.
E ai, gostou? Deu para entender media, moda e mediana? Se gostou compartilha com os amigos. Se ainda ficou alguma dúvida deixe nos comentários.
Quero ficar por dentro das dicas
Cadastre-se aqui e fique por dentro das nossas dicas para passar no ENEM e concursos. Ainda receba as 7 dicas MATADORAS para passar no ENEM.
Fique tranquilo. Nós não enviamos spam


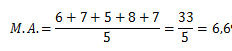
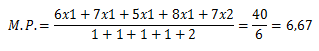
Deixe um comentário