Resoluções – Questões sobre conjuntos

Aqui estão todas as resoluções das questões sobre conjuntos.

Para ver o enunciado das questões clique aqui e para ver a teoria de conjuntos clique aqui.

–

Resoluções questões sobre conjunto

Questão 1

Informações do enunciado:

Total de alunos: 1200

600 alunos falam inglês

500 alunos falam espanhol

300 não falam nenhum idioma

Ele quer saber qual a probabilidade de que o aluno fale somente espanhol?

Definição de probabilidade = (n⁰ de possibilidades favoráveis ÷ n⁰ de possibilidades possíveis)

N⁰ de possibilidade favoráveis = alunos que falam somente espanhol

N⁰ de possibilidades possíveis = total de alunos que não falam inglês

Então o 1⁰ passo será descobrir os alunos que falam somente espanhol. Faremos isso através do diagrama de conjuntos:

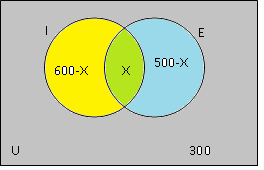
Para montarmos o diagrama, começamos a colocar os valores no diagrama pela interseção, que o n⁰ de alunos que falam inglês e espanhol. Como não sabemos será X.

No conjunto I,a parte amarela será das pessoas que só falam inglês. Sabemos que a quantidade que fala inglês é 600, para saber quem só fala inglês devemos diminuir X.

No conjunto E,a parte azul será das pessoas que só falam espanhol. Sabemos que a quantidade que fala espanhol  é 500, para saber quem só fala espanhol devemos diminuir X.

E as pessoas que não falam nem inglês, nem espanhol ficam do lado de fora desses dois conjuntos como o mostra o diagrama.

A soma de todos esses valores deve ser igual a 1200, ou seja:

600-X+X+500-X+300=1200

1400-X=1200

X=1400-1200

X=200 => essa é a quantidade de alunos que falam inglês e espanhol.

Se que quero saber quem só fala espanhol será 500 -200 =300

Alunos que só falam espanhol = 300

2⁰ passo: Achar o valor total de alunos que não falam inglês = 1200 – 600 = 600

Ou seja o número de possibilidades (alunos que não falam inglês) será 600.

3⁰passo: Substituir os valores na fórmula de probabilidade

P= alunos que só falam espanhol ÷ todos os alunos que não falam inglês

P = 300 ÷ 600

P=1/2

Letra A

Questão 2

Como ele não deu o total de aluno, vamos considerar que o total seja 100, para facilitar as contas, já que as informações estão em percentual.

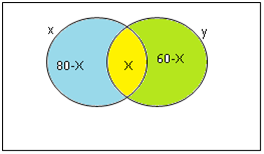
Sempre começamos a fazer exercícios de conjunto pela interseção. Nesse caso, não sabemos quantos leem os dois jornais, por isso vamos chamar de X.

Quem lê somente o jornal X será = 80 – x

E quem lê somente o jornal Y será = 60 – x

O somatório deve dar 100, pois é o total.

80 – x +x – 60 – x = 100

140 – x = 100

x = 40   => Letra c

Questão 3

2ⁿ=subconjuntos

2ⁿ= 1024

2ⁿ= 2¹⁰

n=10

R.: A tem 10 elementos.

Questão 4

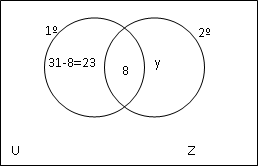
Vamos começar sempre pela interseção. No enunciado é dito, que 31 acertaram a primeira. Então, quem acertou somente a primeiro será igual a 31-8=23

Chamaremos de y, quem acertou somente a segunda e de z quem não acertou nenhuma.

Não sabemos quantos acertaram somente a segunda, mas sabemos que 35 acertaram somente uma questão, então:

23 + y = 35

y = 12

Também não sabemos quantos não acertaram nenhuma, mas sabemos que 40 erraram a segunda. Quem errou a segunda, foi quem errou as duas e quem só acertou a primeira, então:

23+Z = 40

Z = 17

Agora que sabemos todas as partes, podemos somar para saber o total de aluno:

23+8+12+17=60

Letra E

Questão 5

RESOLUÇÃO

C1 = 50

C2 = 45

C3 = 40

C1 ∩ C2 = 10

C1 ∩ C3 = 6

C2 ∩ C3 = 5

C1 ∩ C2 ∩ C3 =4

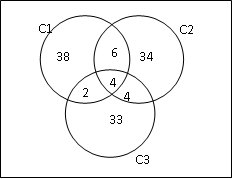
Para montar o diagrama vamos sempre começar da Interseção. Como são 3 conjuntos, começamos por

C1 ∩ C2 ∩ C3 =4, depois vamos para a interseção entre dois conjuntos e descontando o valor que já está na interseção dos 3, e em seguida para somente C1 ou C2 ou C3:

C1 ∩ C2 ∩ C3 = 4

(C2 ∩ C3) – (C1 ∩ C2 ∩ C3) = 5 – 4 = 1

(C1 ∩ C3) – (C1 ∩ C2 ∩ C3) = 6 – 4 = 2

(C1 ∩ C2) – (C1 ∩ C2 ∩ C3) = 10 – 4 = 6

C1 – 4 – 2 – 6 = 50 – 12 = 38

C2 – 4 – 1 – 6 = 45 – 11 = 34

C3 – 4 – 1 – 2 = 40 – 7 = 33

4 + 1 + 2 + 6 + 38 + 34 + 33 = 118

Resposta: 118

Questão 6

Resolução:

Total de empresas = 100

RJ = 52

Exportadora (Exp) = 38

Sociedade Anônima (SA) = 35

RJ ∩ EXP = 12

RJ ∩ SA = 15

EXP ∩ AS = 18

Nem RJ, nem EXP, nem AS = 12

RJ ∩ EXP ∩ AS = ??

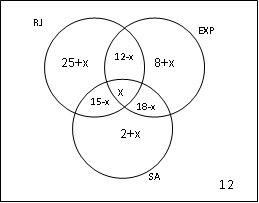
Antes de somar as partes temos que achar somente RJ, somente EXP e somente AS:

Somente RJ = 52 – (15-x) – x – (12-x)

Somente RJ = 52 -15 + x –x -12 +x = 25 +x

Somente EXP = 38 – (12-x) – x – (18-x)

Somente EXP = 38 -12+x –x -18 +x = 8 + x

Somente SA = 35 – (15-x) –x – (18-x)

Somente SA = 35 – 15 +x –x -18 +x = 2 + x

 Agora podemos somar tudo:

25+x + 8+x +2+x+12-x+15-x+18-x+x+12=100

92+x = 100

 x = 8

letra C

Questão 7

Resolução

Total=979

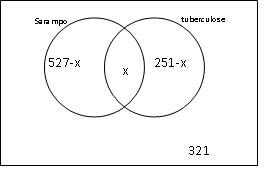
Sarampo= 527

Tuberculose = 251

Sem doença = 321

Com as duas doenças = ?

Somando todos temos: 527 – x + x +251 – x + 321 = 979

1099 – x =979

x = 1099 – 979 = 120

Resp.: 120 prisioneiros tinham as duas doenças.

—