Se você quer mandar bem no ENEM, você tem que estar por dentro de Probabilidade.
Essa matéria cai todo ano e cai mais de uma questão sobre esse tema. Além de ser importante para o ENEM, também cai na maioria dos concursos que tem raciocínio lógico entre as matérias. Essa é a hora de descobrir tudo que precisa sobre probabilidade para mandar bem nessas questões!!
—
PROBABILIDADE
O estudo das probabilidades, cujas ferramentas dão suporte a uma extensa área de conhecimento, teve sua origem na necessidade de quantificar os riscos dos seguros e de avaliar as chances de ganhar em jogos de azar.
—
Fenômeno aleatório
É um fenômeno que pode ser repetido várias vezes e sob as mesmas condições e apresentar resultados diferentes, ou seja, eventos aleatórios definidos pelo acaso.
—-
Alguns exemplos de fenômeno aleatório:
– lançamento de um dado não viciado;
– número de peças defeituosas fabricadas por uma máquina;
– resultado de um jogo de roleta;
—–
Pelo fato de não sabermos o resultado exato de um fenômeno aleatório é que buscamos os resultados prováveis, ou seja, a probabilidade de determinado resultado ocorrer.
—
Espaço Amostral
Em um fenômeno aleatório, o conjunto formado por todos os resultados possíveis é chamado espaço amostral (Ω). Qualquer subconjunto do espaço amostral é chamado de evento.
—
Exemplos:
- Lançamento de um dado
O conjunto de todos os resultados possíveis é {1, 2, 3, 4, 5, 6}
Um subconjunto poderia ser o de números ímpar: {1, 3, 5}
—
- Lançamento de uma moeda
O conjunto de todos os resultados possíveis é: {cara, coroa}
—
Cálculo da probabilidade
A probabilidade de um evento ocorrer será a razão entre os números de resultados favoráveis para esse evento e o número total de resultados possíveis (espaço amostral).
—-
Evento certo, impossível e mutuamente exclusivo
—
-
Evento certo
É quando um evento coincide com o espaço amostral.
—
Exemplos: Ao lançar um dado qual a probabilidade de sair um número menor que 7?
Resultados possíveis: {1, 2, 3, 4, 5, 6} = 6
Resultados favoráveis: {1, 2, 3, 4, 5, 6} = 6
—
Todos os números possíveis de cair são menores que 7, assim esse é um evento certo, pois a probabilidade é de 100% de ocorrer.
p(A) = 6 ÷ 6
p(A) = 1 ou 100%
—
-
Evento impossível
É quando um evento é vazio, ou seja, ele não está dentro do espaço amostral.
—
Exemplos: Ao lançar um dado qual a probabilidade de sair um número maior que 6?
Resultados possíveis: {1, 2, 3, 4, 5, 6} = 6
Resultados favoráveis: { ᴓ} = 0
—
No espaço amostral não existe número maior que 6, assim esse é um evento impossível, pois tem probabilidade de 0% de ocorrer.
p(A) = 0 ÷ 6
p(A) = 0 ou 0%
—
-
Eventos mutuamente exclusivos
É quando a intersecção de dois eventos é um conjunto vazio.
—
Exemplo: Ao lançar um dado qual a probabilidade de cair um número ímpar e um múltiplo de 2.
Resultados possíveis: {1, 2, 3, 4, 5, 6}
Resultados favoráveis:
Evento 1 – ser número ímpar: {1, 3, 5}
Evento 2 – ser múltiplo de 2: {2, 4, 6}
—
Como ele quer saber a probabilidade de cair um número ímpar E um múltiplo de 2. Será a intersecção entre o evento 1 e o evento 2. Como não existe nenhum número que esteja nos dois subconjuntos, a intersecção entre eles é um conjunto vazio.
Evento 1 ∩ Evento 2 = ᴓ.
p(A) = 0 ÷ 6
p(A) = 0 ou 0%
—
Intersecção de eventos
É quando tendo dois ou mais eventos, queremos saber a probabilidade de sair um número que está em todos os subconjuntos. O que determina a intersecção é a existência da palavra E.
—
Exemplo: Ao lançar um dado, qual a probabilidade de sair um número par e um número múltiplo de 3.
Resultados possíveis: {1, 2, 3, 4, 5, 6}
—
Resultados favoráveis: Evento 1 ∩ Evento 2
Evento 1 – ser número par: {2, 4, 6}
Evento 2 – ser múltiplo de 3: {3, 6}
Evento 1 ∩ Evento 2 = {6}
—
Probabilidade = (Evento 1 ∩ Evento 2) ÷ Espaço Amostral
Probabilidade = 1/6
—
—
União de eventos
É quando tendo dois ou mais eventos, queremos saber a probabilidade de sair um número que pode estar em qualquer um dos conjuntos. O que determina a união é a existência da palavra OU.
—
Exemplo: Ao lançar um dado, qual a probabilidade de sair um número par ou um número múltiplo de 3.
Resultados possíveis: {1, 2, 3, 4, 5, 6}
—
Resultados favoráveis: Evento 1 U Evento 2
Evento 1 – ser número par: {2, 4, 6}
Evento 2 – ser múltiplo de 3: {3, 6}
Evento 1 U Evento 2 = {2, 3, 4, 6}
—
Probabilidade = (Evento 1 U Evento) ÷ Espaço Amostral
Probabilidade = 4/6
—
É importante frisar que a probabilidade da união de dois eventos(A e B) será:
p(A U B) = p(A) + p(B) – p(A ∩ B)
—
Ou seja, será a probabilidade de A ocorrer mais a probabilidade de B ocorrer, menos o conjunto de resultados que eles tem em comum.
—
No exemplo acima vamos chamar o evento 1 de A e o evento 2 de B, assim teremos:
p(A) = 3/6
p(B) = 2/6
p(A ∩ B) = 1/6 ( a intersecção de A e B é o subconjunto 6)
p(A U B) = 3/6 + 2/6 – 1/6
p(A U B) = 4/6
—
Probabilidade Condicional
É quando temos dois eventos A e B, em que o evento A depende do fato de que o evento B ocorreu. É definida por p(A/B), ou seja, a probabilidade condicional de ocorrer A, tendo ocorrido B.
—
Exemplo: Ao lançar uma moeda 3 vezes, qual a probabilidade de sair cara duas vezes, sabendo que o resultado do primeiro lançamento foi cara?
—
Vamos chamar o evento de sair cara duas vezes de A e o evento sair cara no primeiro lançamento de B. E chamaremos cara = c e coroa = C.
—
Assim, espaço amostral, ou seja, todos os resultados possíveis ao lançar um moeda 3 vezes:
{CCC, CCc, CcC, Ccc, cCC, cCc, ccC,ccc} = 8
Os resultados favoráveis para A são: {ccC, cCc, Ccc} = 3
Os resultados favoráveis para B são: {ccc, ccC, cCc, cCC} = 4
—
p(B) = 4/8 => p(B)=1/2
p(A ∩ B)= 2/8 (pois existem 2 termos em comum nos conjuntos A e B)
p(A ∩ B)=1/4
Aplicando a fórmula da probabilidade condicional temos:
—
Eventos Independentes
É quando temos dois eventos A e B, e a probabilidade de ocorrer um deles não depende do fato de ter ocorrido ou não o outro. Assim, a probabilidade de A e B ocorrem será dada por:
p(A ∩ B) = p(A) . p(B)
—
Exemplo: Ao lançar 2 dados não viciados, qual a probabilidade de sair 6 no primeiro dado e sair 3 no segundo dado?
—
Chamaremos de A o evento de sair 6 no primeiro dado e B o evento de sair 3 no segundo dado.
p(A) = números de resultados favoráveis(A) ÷ números de resultados possíveis(A)
números de resultados favoráveis(A) = 1 (sair 6)
números de resultados possíveis(A) = 6 ({1,2,3,4,5,6})
—
p(A) = 1/6
—
p(B) = números de resultados favoráveis(B) ÷ números de resultados possíveis(B)
números de resultados favoráveis(B) = 1 (sair 3)
números de resultados possíveis(B) = 6 ({1,2,3,4,5,6})
—
p(B) = 1/6
—
A probabilidade de acontecer o evento A e o Evento B será p(A ∩ B) = p(A) . p(B)
—-
Com essas informações cobrimos tudo que você precisa saber sobre probabilidade. Agora é colocar em prática. Se ainda ficou alguma dúvida deixe nos comentários.
–é
Gostou do artigo? Se sim, compartilhe com seus amigos!! Até a próxima e bons estudos.
Quero ficar por dentro das dicas
Cadastre-se aqui e fique por dentro das nossas dicas para passar no ENEM e concursos. Ainda receba as 7 dicas MATADORAS para passar no ENEM.
Fique tranquilo. Nós não enviamos spam




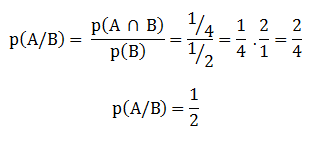
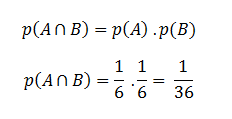
Deixe um comentário