Números racionais x Números irracionais – Você sabe a diferença??
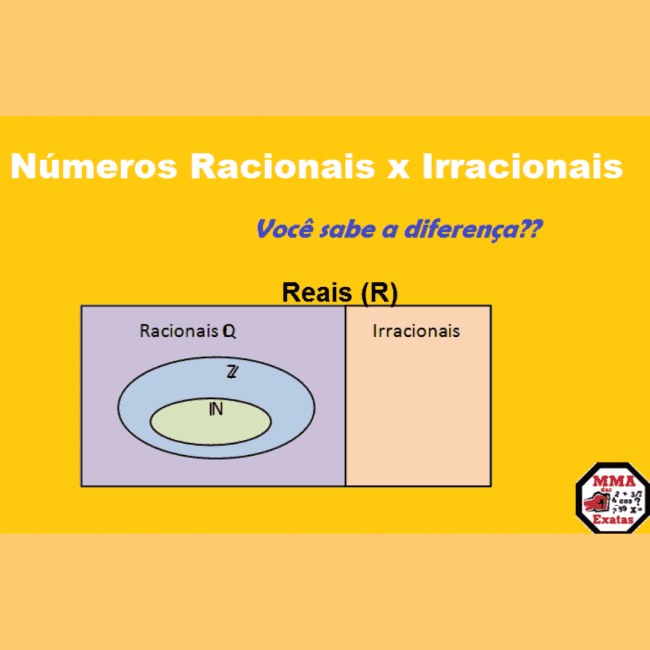
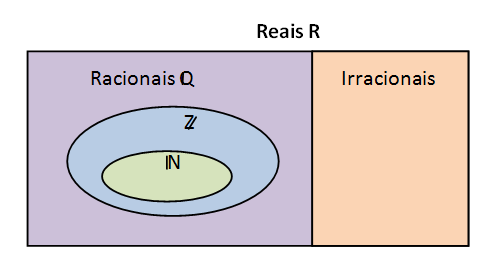
O conjunto dos números Reais (R) é formado pela união dos números racionais e os números irracionais. Pelo diagrama abaixo podemos observar:
Hoje vamos estudar os conjuntos dos números Racionais e Irracionais e entender a diferença entre eles. Em outro artigo vamos falar mais sobre os conjuntos dos Naturais e Inteiros.
–
Números Racionais
—
Números que podem ser expressos na forma a/b, em que a e b são inteiros e b ≠ 0, são chamados números racionais. Em outras palavras, são racionais os números que são razões (quocientes) de dois números inteiros.
Simbolicamente, representa-se o conjunto dos números racionais (Q) assim:
São números racionais:
—
– Qualquer número inteiro.
Exemplos:
a) 0 = 0/3
b) 5 = 5/1
c) 10 = 20/2
d) -8 = -8/1
De modo geral, os números inteiros podem assumir a forma a/b, na qual a ϵ Z, b ϵ Z* e a é múltiplo de b.
– Qualquer decimal exato (numerais que apresentam um número finito de algarismos decimais diferentes de zero).
Exemplos:
a) 6,3 = 63/10
b) -0,0001 = -1/10.000
c) 6,171717 = 6171717/106
d) 4,3 = 4,30 = 4,300 = 4,3000 = … é um decimal exato
– Qualquer fração de numerador inteiro e de denominador inteiro não nulo.
Exemplos:
a) -1/8
b) 7/13
c) 31333/990
– Qualquer decimal periódico (numerais formados por infinitos algarismos decimais que se repetem periodicamente).
Exemplos:
a) 0,666…
b) -0,232323…
c) 5,1888…
Ficou claro?? Agora vamos para os números irracionais…
—
Números Irracionais
Números como 1,4142135…, cuja representação decimal é infinita e não periódica, são chamados de números irracionais, isto é não racionais e, sendo assim, não são inteiros nem razão de dois inteiros, mas podem representar medidas no mundo real, como a medida da diagonal do quadrado de lado 1.
Veja outros exemplos de números irracionais:
a) 0,1234567891011…
b) 1,01002000300004…
c) π = 3,141592…
d) raiz de 3 = 1,7320508…
—
Ficou claro a diferença entre esses dois conjuntos?? Então vamos praticar. Separei alguns exercícios para você entrar em ação. Se ficou alguma dúvida, deixe nos comentários que vou responder.
Exercícios Propostos Números Racionais x Números Irracionais
1) Escreva R para número racional e I para número irracional
a) ( ) 8
b) ( ) 3,172737…
c) ( ) -3,0100100001…
d) ( ) -5,411769
e) ( ) -3,222…
f) ( ) -3,24681012…
g) ( ) raiz de 7
h) ( ) 2,4111…
i) ( ) 0
2)Dos números a seguir, o único irracional é
3) Com relação ao conjunto dos números reais e seus subconjuntos, analise as sentenças seguintes e assinale V para verdadeiro e F para falso.
( ) Todo número irracional é real
( ) Raiz quadrada de 9 é irracional
( ) Raiz quadrada de 3 é real
( ) O zero é irracional
Respostas Exercícios Propostos
- Resp.: R, I, I, R, R, I, I, R, R
- Resp.: d)
- Resp.: V, F, V, F
Quero ficar por dentro das dicas
Cadastre-se aqui e fique por dentro das nossas dicas para passar no ENEM e concursos. Ainda receba as 7 dicas MATADORAS para passar no ENEM.
Fique tranquilo. Nós não enviamos spam
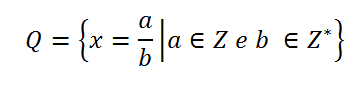
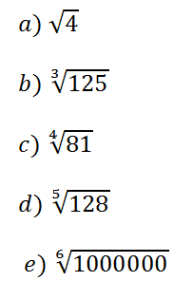
Alessandra Vargas da Silveira
3- Escreva R para número número irracional a) () 8 b) () 2,236067977499… ( )- c) 1,732050807568.. d) () raiz de 961 e) ()-3 f) () -2,236067977499… g) () raiz de 7 h) () raiz de 289 racional e I para i) ( ) 0