Hoje vamos estudar Conjuntos. Esse é um tópico importante tanto para quem vai estudar para o ENEM e vestibulares, quanto para quem está estudando para concursos. Conjunto é uma matéria recorrente nas provas, por isso se você souber como resolver já garante alguns pontinhos a mais na sua nota. Então vamos começar!!
—
Conjuntos
A ideia de conjunto se relaciona a ideia de grupo ou coleção.
Ex.: Conjunto dos dias da semana
D={Domingo, Segunda, Terça, Quarta, Quinta, Sexta, Sábado}
-
Quando o conjunto for vazio deve ser representado por:
C= { } ou C= Ø
-
Se o conjunto tem mais elementos colocamos (…) para indicar que ele continua.
ELEMENTO de um conjunto
-
Cada uma das partes individuais deste conjunto é chamada de elementos.
Ex.: V={ a, e, i, o, u}
a, e, i, o, u são elementos de V
—
a ϵ V – a é elemento de V
b ∉ V – b não é elemento de V
—
-
Um conjunto (quando for possível) também pode ser descrito através de uma propriedade comum a todos os seus elementos.
Ex.: V= {x ϵ V/ x é uma vogal}
—
-
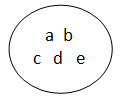
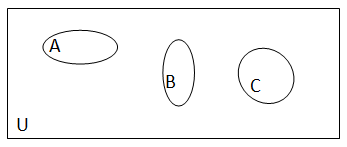
Ou através de um diagrama
—
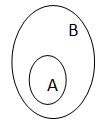
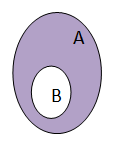
Subconjunto
Imagine dois conjuntos A e B. Se todo elemento de A for também elemento de B, então A é subconjunto de B.
-
Todo subconjunto é subconjunto de si mesmo
A C A
-
O vazio é subconjunto de qualquer conjunto.
Imagine o conjunto A={1, 3, 5, 7, 9}.
As seguintes afirmações são verdadeiras.
{1, 3, 5} C A {1, 2} A
{1} C A {9, 7, 5, 3, 1} C A
1 ⊅ A Ø ⊅ A
—
Número de subconjuntos de um conjunto
Para um conjunto de n elementos, temos que o número de subconjuntos formados será 2n
Ex.: B={1, 2, 3} n= 3
Subconjuntos = 23= 8
Como podemos ver os subconjuntos são: {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1, 2, 3}, Ø
Diferença entre subconjunto e elemento
– Subconjunto: é um conjunto feito a partir de um conjunto original.
– Elemento: Integrante de um conjunto.
Se o elemento a faz parte do conjunto B, então: a ϵ B e {a} C B
—
CONJUNTOS NÚMERICOS
-
Números naturais
São os números que usamos para contar objetos.
N = {0,1,2,3,4…}
-
Números inteiros
São os números inteiros positivos e negativos e zero.
Z = {…-3,-2,-1,0,1,2,3…}
—
Z+= conjunto dos inteiros positivos e o zero
Z –= conjunto dos inteiros negativos e o zero
Z+*= conjunto dos inteiros positivos, SEM o zero
Z* –= conjunto dos inteiros negativos, SEM o zero
- Números Racionais
Sejam a e b dois números inteiros, com b≠0. Em outras palavras, são racionais os números que são razões (quocientes) de dois números inteiros. Assim, simbolicamente, representa-se o conjunto dos números racionais (Q) da seguinte forma:
São números racionais:
- Qualquer número inteiro.
Exemplos:
a) 0 = 0/3
b) 5 = 5/1
c) 10 = 20/2
d) -8 = -8/1
De modo geral, os números inteiros podem assumir a forma a/b, na qual a ϵ Z, b ϵ Z* e a é múltiplo de b.
- Qualquer decimal exato (numerais que apresentam um número finito de algarismos decimais diferentes de zero).
Exemplos:
a) 6,3 = 63/10
b) -0,0001 = -1/10.000
c) 6,171717 = 6171717/106
d) 4,3 = 4,30 = 4,300 = 4,3000 = … é um decimal exato
- Qualquer fração de numerador inteiro e de denominador inteiro não nulo.
Exemplos:
a) -1/8
b) 7/13
c) 31333/990
- Qualquer decimal periódico (numerais formados por infinitos algarismos decimais que se repetem periodicamente).
Exemplos:
a) 0,666…
b) -0,232323…
c) 5,1888…
-
Números Irracionais
Números como 1,4142135…, cuja representação decimal é infinita e não periódica, são chamados de números irracionais, isto é não racionais e, sendo assim, não são inteiros nem razão de dois inteiros, mas podem representar medidas no mundo real, como a medida da diagonal do quadrado de lado 1.
Veja outros exemplos de números irracionais:
a) 0,1234567891011…
b) 1,01002000300004…
c) π = 3,141592…
d) raiz de 3 = 1,7320508…
—
NÚMEROS REAIS
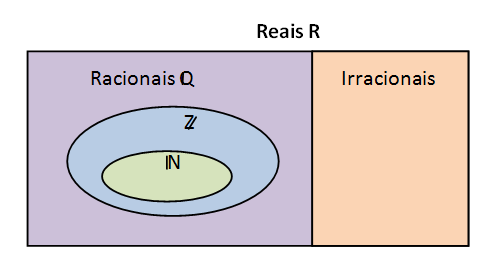
O conjunto dos números Reais (R) é formado pela União dos números racionais e os números irracionais.
Usando o diagrama temos:
—
Conjunto UNIVERSO
É o conjunto que engloba todos os conjuntos considerados.
OBS.: O conjunto Universo poderá limitar as soluções de um problema.
Ex: Qual a solução de X+1=2,5? Considere U= números naturais.
X=2,5-1
X=1,5, Mas 1,5 ∉ Naturais
Resp.: Não há solução, pois a resposta está fora do conjunto universo citado.
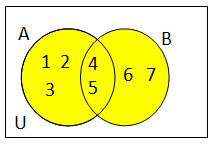
União de conjuntos
É a junção dos elementos de dois ou mais conjuntos. Símbolo: U
Ex.: A= {1,2,3,4,5} B={4,5,6,7}
AUB={1,2,3,4,5,6,7}
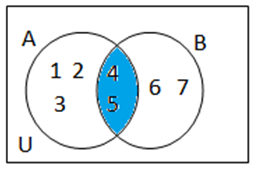
Intersecção de conjuntos
São os elementos comuns a 2 ou mais conjuntos. Símbolo: ∩
Ex.: A= {1,2,3,4,5} B={4,5,6,7}
IMPORTANTE: Quando formos resolver questões de conjunto, devemos SEMPRE começar pela interseção.
Propriedades dos conjuntos
- A UA=A => propriedade idempoente
- Ø U A = A => elemento neutro da união
- A U (BUC) = (A U B) U C => propriedade associativa
- A U B = B U A => propriedade comutativa
- A ∩ A =A => propriedade idempoente
- A ∩ B = B ∩ A => propriedade comutativa
- A ∩ (B ∩ C) = (A ∩ B) ∩ C => propriedade assossiativa
- A ∩ (B U C) = (A ∩ B) U (A ∩ C) => propriedade distributiva
- A U (B ∩ C) = (A U B) ∩ (A U C) => propriedade distributiva
—
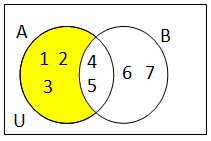
SUBTRAÇÃO de conjuntos
Dados dois conjuntos A e B, a diferença A – B é o conjunto formado pelos elementos que fazem parte de A, mas não fazem parte de B.
Ex.: A= {1,2,3,4,5} B={4,5,6,7}
A – B = {1, 2, 3}
B – A = {6,7}
—
COMPLEMENTAR
Sejam A e B dois conjuntos onde B é subconjunto de A. Define-se o complementar de B em relação A como sendo A – B.
CAB = A –B
Ex.: A= {1,2,3,4,5,6,7} B= {2,4,6}
CAB={1,3,5,7}
OBS.: Só é complementar quando um conjunto é subconjunto do outro.
Agora você já sabe tudo que precisa para começar a resolver as questões de conjuntos. Cadastre-se na nossa lista e receba várias dicas e materiais que vão te ajudar nos seus estudos. Se gostou compartilhe com seus amigos. Se quiser uma apostila para estudar Raciocínio Lógico Matemático clique aqui.
Se ainda ficou com dúvidas deixe um cometário que te responderei o mais rápido possível.
Quero ficar por dentro das dicas
Cadastre-se aqui e fique por dentro das nossas dicas para passar no ENEM e concursos. Ainda receba as 7 dicas MATADORAS para passar no ENEM.
![]() Fique tranquilo. Nós não enviamos spam
Fique tranquilo. Nós não enviamos spam


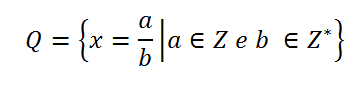
Deixe um comentário